- Las matemáticas financieras constituyen una disciplina especializada dentro del campo de las matemáticas.
- El enfoque es en el análisis y la gestión de transacciones financieras e inversiones.
¿Qué Son Las Matemáticas Financieras?
Utilizar fórmulas matemáticas financieras permite evaluar correctamente diversas operaciones económicas, tales como:
- Inversiones
- Bonos
- Prestamos
- Seguros
- Activos mobiliarios e inmobiliarios
También es crucial en la activad financiera en lo que respecta a la previsión de flujos y rendimientos y específicamente en:
- Gestión de riesgos
- Optimización de una cartera de inversiones
- Análisis de rendimientos futuros
- Relación entre rendimiento y riesgo
- Valoración de flujos de dinero
Además, las matemáticas financieras son importantes en la vida cotidiana para entender y valorar los productos financieros que consumimos. Las fórmulas matemáticas financieras se aplican a todos los instrumentos, como:
- Hipoteca
- Tarjetas de crédito
- Préstamos personales
- Fondos
Aplicar las fórmulas matemáticas financieras a estos instrumentos nos permite evaluar correctamente una oferta respecto a otra y el coste real de cada operación.
Fórmulas Matemáticas Financieras Comunes
A continuación, se presentan algunas de las fórmulas matemáticas financieras más comunes, utilizadas en contextos económicos y de inversión:
Tasa de Interés Simple
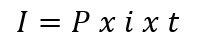
Donde:
- P = Capital inicial
- i = Tasa de interés por periodo
- t = Número de periodos
Tasa de Interés Compuesto
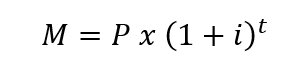
Donde:
- M = Monto
- P = Capital inicial
- i = Tasa de interés por periodo
- t = Número de periodos
Valor Futuro (VF) de una inversión
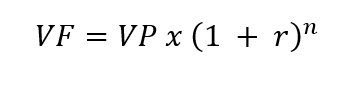
Donde:
- VF = Valor futuro
- VP = Valor presente
- r = Tasa de interés por período
- n = Número de períodos
Valor Presente (PV) de una inversión o Flujo de Efectivo
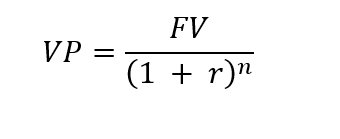
Donde:
- VF = Valor del flujo de efectivo esperado
- VP = Valor presente
- r = Tasa de descuento por período
- n = Número de períodos
Tasa Interna de Retorno (TIR)
La TIR es el rendimiento de una inversión donde se evalúa los flujos de caja, positivos y negativos. Permite comparar diferentes tipos de inversiones de manera uniforme. Se calcula resolviendo la siguiente formula:
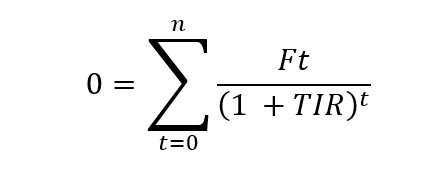
Donde:
- Ft = Flujo de efectivo en el periodo t
- TIR = Tasa interna de retorno
Tasa de interés Nominal (TIN) a Efectiva (TIE)
La TIE toma en consideración el efecto del interés compuesto y se calcula utilizando la siguiente fórmula:
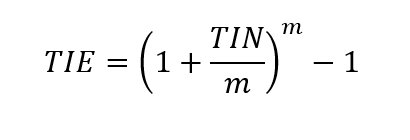
Donde:
- TIE = Tasa de interés efectiva
- TIN = Tasa de interés nominal
- m = Número de periodos de capitalización por año
Pago Constante (PMT) en un Préstamo o Anualidad
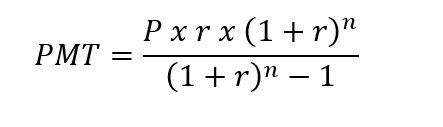
Donde:
- PMT = Pago por periodo
- P = Cantidad inicial del préstamo
- r = Tasa de interés por período
- n = Número total de pagos
Valor Actual Neto (VAN) de un Proyecto de Inversión
El valor de un proyecto de inversión se puede evaluar utilizando esta métrica. Se calcula restando el costo inicial del proyecto (o inversión) de la suma de los flujos futuros en efectivo, descontados a una tasa de descuento apropiada.
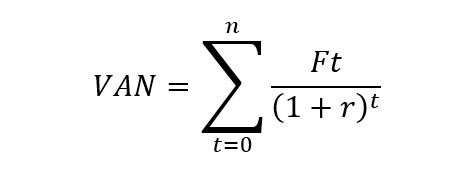
Donde:
- VAN = Valor actual neto
- ft = Flujo de efectivo en el periodo t
- r = Tasa de descuento o costo de capital
Ejemplos Con Fórmulas Matemáticas Financieras
Vamos a considera unos ejemplos de como se utilizan las matemáticas financieras en la vida real.
Préstamo Personal
Cristina ha solicitado un préstamo bancario de $10,000 a una tasa anual de 15% durante 5 años. Las condiciones del contrato de préstamo establecen que se pagaran cuotas constantes todos los meses hasta amortizar el capital más los intereses.
Datos:
- Monto del préstamo (P) = $10,000
- Tasa de interés por periodo (r) = 15%/12
- Número de períodos (n) = 12 x 5 = 60
Para calcular el pago mensual de este préstamo vamos a utilizar la fórmula:
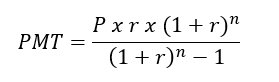
Sustituyendo: PMT = ($10,000 x 0.15/12 x (1 + (0.15/12))^60) / (((1+(0.15/12))^60)-1 = $237.89
Cristina ha podido acertarse que la cifra propuesta por el banco es correcta. Además, podría realizar un simulacro para evaluar qué plazos o importes de préstamo podrían ser más convenientes para ella.
Rentabilidad de un Fondo
Pablo está considerando invertir $20,000 en un fondo de bonos que paga un interés anual del 8%. ¿Cuánto dinero va a tener Pablo después de 5 años de inversión, si el interés se capitaliza anualmente?
Datos:
- Capital inicial (P) = $20,000
- Tasa de interés anual (i) = 8%
- Numero de años (períodos) = 5
Para calcular la rentabilidad de esta inversión utilizaremos la siguiente fórmula:
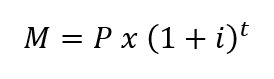
Sustituyendo: M = $20,000 x (1 + 0.08)^5 = $29,386.56
Pablo ha podido conocer el monto de intereses más capital después de 5 años con los intereses capitalizados. También, podría comparar la misma inversión al 8% anual sin dejar los intereses en el fondo. Para ello, solo tendría que utilizar la fórmula para intereses simples.
Herramientas Avanzadas en Matemáticas Financieras
Vamos a explorar algunas herramientas avanzadas utilizadas en matemáticas financieras para el análisis y gestión de:
- Inversiones
- Carteras
- Gestión de riesgo
- Instrumentos financieros
Series Temporales Financieras
Las series temporales financieras se analizan para modelar y predecir el comportamiento de variables financieras. Estas variables incluyen:
- Precios de acciones
- Tasas de interés
- Rendimientos de inversiones
Se utilizan técnicas como ARIMA (Auto-regresive Integrated Moving Average) y GARCH (Generalized Autoregressive Conditional Heteroskedasticity) para identificar patrones y tendencias en la rentabilidad financiera.
Optimización de Carteras
Las matemáticas financieras se utilizan para construir carteras de inversión óptimas con respecto a rendimiento y riesgo. Se trata de maximizar el rendimiento de la cartera dado un nivel especifico de riesgo.
También, se puede minimizar el riesgo de la cartera dado un nivele especifico de rendimiento. Para llegar a estos objetivos, se utilizan técnicas como la teoría moderna de carteras (MPT) y el modelo de asignación de activos basado en la teoría de Markowitz.
Gestión de Riesgo
Los modelos de riesgo permiten a los inversionistas y instituciones financieras cuantificar y gestionar los riesgos asociados con:
- Inversiones
- Carteras
- Instrumentos financieros
Entre los modelos más comunes se encuentran:
- Valor en Riesgo (VaR): El VaR es un método estadístico que toma en cuenta la posible pérdida máxima que podría experimentar una inversión durante un período especifico.
- Estándar de Riesgo (ES) o Pérdida Esperada: El Estándar de Riesgo es la cuantía de dinero a riesgo en el peor escenario posible. Por ejemplo, en el caso de un evento catastrófico.
- Simulación de Montecarlo: Este modelo genera múltiples escenarios de posibles rendimientos de mercados e inversiones financieras para evaluar el riesgo.
- Modelo de Ajuste de Cola (TVaR): EL TVaR mide el riesgo de las posibles pérdidas en los casos de que el VaR sea superado.
Conclusión
Las matemáticas financieras son una herramienta indispensable tanto para profesionales como para particulares en la gestión y evaluación de inversiones financieras. Su aplicación abarca desde la valoración de rendimientos hasta la gestión de riesgos.
Además, las matemáticas financieras son importantes también en la vida cotidiana. Desde evaluar diferentes opciones de préstamos o hipotecas hasta comprender el impacto de las tasas de interés compuestas o simples.
